Warfarin is an essential anticoagulant with a narrow therapeutic index. It is one of widely prescribed anticoagulants such as: aspirin, dabigatran, rivaroxaban, apixaparin, lovenox, fondaparinux and heparin. Commercially available warfarin is a racemic mixture of two enantiomers that are extensively metabolized in liver. Warfarin is commonly used for prophylaxis and treatment of venous and arterial thrombosis [1-11].

The current study is a companion piece of the related study by Colburn published in August 1973 Issue of the Journal Pharmacokinetics and Bio pharmaceutics. Therefore, the data from the study cited here were used [1]. For modeling purposes, an advanced mathematical modeling method based on the theory of dynamic systems was employed, see for example the following studies [12- 27] and references therein. The goal of the current study was to continue presenting some interesting views on a successful use of an advanced modeling method based on the theory of dynamic systems in pharmacokinetics.

Previous examples showing how an advanced modeling method used in the current study can be employed in various pharmacokinetic studies can found in the full text articles, authored and/or co-authored by the author of the current study, which can be downloaded free of charge from the following web page of the author: http://www.uef.sav.sk/advanced.htm.

The data from the study by Colburn [1] were used. As stated above, an advanced mathematical modeling method based on the theory of dynamic systems [12-27] was employed for modeling purposes. Throughout the current study, the lower case letter “S” denoted the complex Laplace variable. The development of a mathematical model of the dynamic system H was performed in the following successive steps:

First, the dynamic system, denoted by H was defined using: 1) the Laplace transform of the mathematically approximated the subject’s plasma concentration-time profile of warfarin after the intravenous administration of warfarin, denoted by C(s), and considered the output of the pharmacokinetic dynamic system H and 2) the Laplace transform of the mathematically approximated the intravenous administration of warfarin to a subject [1], denoted by I(s), and considered the warfarin input to the subject’ body and/or to the dynamic system H [13- 28]. In the following text, the pharmacokinetic dynamic system H, was simply called the dynamic system.

Second, the following simplifying assumptions were made: a) initial conditions of the dynamic system H were zero; b) pharmacokinetic processes occurring in the subject’s body after the intravenous administration of warfarin were linear and time invariant [13-27]; c) concentrations of warfarin were the same throughout all subsystems of the dynamic system (where a subsystem was an integral part of the dynamic system H); d) no barriers to the distribution and /or elimination of warfarin existed; e) the dynamic system H was stable them and did not become unstable during the time course of the study published previously [1] and the current study.

Third, the dynamic system H was used to mathematically describe static and dynamic properties [28-31] of the pharmacokinetic behavior of warfarin in a subject [1]. Fourth, the transfer function, denoted by H(s) of a the dynamic system was derived using: 1) the Laplace transform of the mathematically approximated plasma concentration-time profile of warfarin of a subject, denoted by C(s), and considered the output of the dynamic system H, and 2) the Laplace transform of the mathematically approximated intravenous administration of warfarin to a subject and considered warfarin input I(s), to the subject’s body and/or to the dynamic system H [12-28], see the following equation:

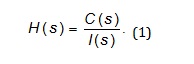
Fifth, the dynamic system H was approximated with the transfer function, denoted by H(s).

Sixth, the computer program named CTDB [13] and the transfer function model HM(s) approximated by Eq. (2), were used to develop a mathematical model of the dynamic system H [12-27].

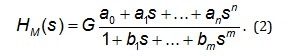
On the right-hand-side of Eq. (2) is the Padé approximant [29,30] of the transfer function model HM(s) G is an estimator of the model parameter called a gain of a dynamic system, a₁… a_n, b₁… b_m are additional model parameters, n is the highest degree of the nominator polynomial, and m is the highest degree of the denominator polynomial, where n

Seventh, the transfer function H(s) was converted into the equivalent frequency response function, denoted by F(iω_j) [13-26].

Eighths, the non-iterative method published previously [29] was used to develop a mathematical model of frequency response function, F_M(iω_j) described by Equation 3, and to determine point estimates of parameters of the frequency response function model FM (iωj) in the frequency domain [13-26].

Analogously as in Eq. (2), n is the highest degree of the numerator polynomial of the frequency response function model F_M(iω_j) m is the highest degree of the denominator polynomial of the frequency response function model F_M(iω_j) where n≤m, i is the imaginary unit, and ω is the angular frequency in Eq. (3).

Ninth, the Akaike information criterion (AIC), modified for the use in the complex domain [14] was used to select the best model of the frequency response function F_M(iω_j) and to determine point estimates of the parameters of the best model of the frequency response function F_M(iω_j) in the complex domain. After that, the Monte-Carlo and the Gauss-Newton method [31-33] were used to refine the best model of the frequency response function F_M(iω_j) and to determine 95 % confidence intervals of the parameters of the model of the frequency response function F_M(iω_j) in the time domain.

After the development of a mathematical model of the dynamic system H, the following potentially important pharmacokinetic variables were determined: the elimination half-time of warfarin, denoted by t_1/2 , the area under the plasma concentration-time profile of warfarin from time zero to infinity, denoted by AUC0_-∞, the total body clearance of warfarin, denoted by Cl. The maximum serum concentration of warfarin, denoted by C_max, was read directly from the plasma concentrationtime profile of warfarin of the subject.

The best-fit third-order model, F_M(iω_j) selected using AIC, is described by the following equation:

This third-order model provided an adequate fit to the warfarin plasma concentration-time profile of warfarin [1] Estimates of the model parameters G, a₀, a₁, b₁, b₂, b₃ are in Table 1.

Model-based estimates of potentially important pharmacokinetic variables of warfarin are in Table 2.

Figure 1 illustrates the observed plasma concentration time profile of warfarin and the description of the observed profile with the developed model of the dynamic system which mathematically approximated dynamic and static properties of the pharmacokinetic behavior of warfarin in the subject investigated [1]. Model-based estimates of potentially important pharmacokinetic variables of warfarin are listed in (Table 2).

The most general form of a model of a frequency response function F_M(iω_j), which was used in the current study is described by Eq. (4). The transfer function model HM(s) and the frequency response function model F_M(iω_j) are implemented in the computer program CTDB [13]. A demo version of the computer program CTDB is available at: http://www.uef.sav.sk/advanced.htm.

The dynamic system used in the current study was a mathematical object, without any physiological significance. It was used to mathematically approximate static and dynamic properties of the pharmacokinetic behavior of warfarin in the subject investigated [1,34-36]. The advanced modeling method used in the current study has been described in detail in the previous studies authored and/or co authored by the author of the current study [13-26], therefore the model description has not been given here.

Analogously as in the studies published previously [13- 26], the development of a mathematical model the dynamic system was based on the known input and output of the dynamic system under study, in the current study. In general, if a dynamic system is modeled using a transfer function model; as it was the case in the current study (see Eq. (2)), then the accuracy of the model depends on the degrees of the polynomials of the transfer function model used to fit the data, see for example the following studies [13-26] and references therein.

The parameter gain is called also a gain coefficient, and/or a gain factor. In general, a parameter gain is defined as a relationship between a magnitude of an output of a dynamic system output to a magnitude of a dynamic system input in steady state. Or in other words, a parameter gain of a dynamic system is a proportional value that shows a relationship between a magnitude of a dynamic system output to a magnitude of a dynamic system input in steady state. The pharmacokinetic meaning of a parameter gain depends on the nature of the dynamic system under study; see for example full text articles available free of charge at: http://www.uef.sav.sk/advanced.htm. The non-iterative modeling method described in the study published previously [29] and used in the current study enables quick identification of an optimal structure of a model of a frequency response. It is a great advantage of this method, because it significantly speeds up the development of frequency response models.

The reason for conversion of H_M(s) to F_M(iω_j) has been explained in the studies published previously; see for example the studies [20-26], therefore an explanation was not given in the current study. The mathematical model developed in the current study sufficiently described static and dynamic properties [34-36] of the pharmacokinetic behavior of warfarin in the subject investigated [1]. The current study showed again that a mathematical modeling method based on the theory of dynamic systems can be successfully used in mathematical modeling in pharmacokinetics.

Frequency response functions are complex functions, therefore modeling must be performed in the complex domain. In general, modeling methods used to develop mathematical models of frequency response functions are computationally intensive. Furthermore, the methods considered require at least a partial knowledge of the theory of dynamic system, and an abstract way of thinking about a dynamic system under study.

The principal difference between traditional pharmacokinetic modeling methods and modeling methods that use of modeling and computational tools from the theory of dynamic systems can be explained as follows: the former methods are based on mathematical modeling plasma and/or blood concentration-time profiles of drugs administered, however the latter methods are based on mathematical modeling dynamic relationships between a mathematically described a drug administration and a mathematically described resulting plasma (or/or blood) concentration-time profiles of drugs administered. See, for example, the full text articles and an explanatory picture, available free of charge at the following web page of the author: http://www.uef.sav.sk/advanced.htm.

The computational and modeling methods that use computational and modeling tools from the theory of dynamic systems can be used for example for adjustment of a drug (or a substance) dosing, aimed at achieving and then maintaining required drug (or a substance) concentration–time profile in a patient see the following study [17]. Moreover, the methods considered here can be used for safe and cost-effective individualization of dosing of a drug or a substance, for example using computer-controlled infusion pumps [37,38]. This is very important for example for an administration of a clotting factor to a hemophilia patient, as exemplified in the simulation study [17].

The advantages of the model and modeling method used in the current study are evident here: The models developed overcome the well known limitations of compartmental models: For the development and use of the models considered here, an assumption of well-mixed spaces in the body (in principle unrealistic) is not necessary. The basic structure of the models is broadly applicable. Therefore, this structure can be used in the development of mathematical models not only in the field of pharmacokinetics but also in several other scientific and practical fields. From a point of view of the pharmacokinetic community, an advantage of the models developed using computational tools from the theory of dynamic systems is that the models considered here emphasize dynamical aspects of the pharmacokinetic behavior of an administered drug in a human and/or in an animal body. Transfer functions of dynamic systems are not unknown in pharmacokinetics; see for example the following studies [37,38]. In pharmacokinetics, transfer functions are usually called disposition functions [39,40]. An anticoagulant therapy is a medication that affects the blood clotting process. Therefore anticoagulants and the knowledge of pharmacokinetics of anticoagulants are important for medical practice. The author assumes that the current study may contribute to the knowledge base in pharmacokinetics.

The model developed and used in the current study successfully described the pharmacokinetic behavior of warfarin in the subject investigated [1] after the intravenous administration warfarin. The modeling method used in the current study is universal; therefore it is applicable to any kind of a dynamic system, not only in the field of pharmacokinetics but also in many other scientific or practical fields. The current study again showed that a mathematical modeling method based on the theory of dynamic systems can be advantageously used in pharmacokinetic modeling. To see the previous examples illustrating the successful use of the modeling method employed in the current study please visits the author’s web page (an English version): http://www.uef.sav.sk/advanced.htm. The current study reaffirmed that an integration of key concepts from pharmacokinetic and bioengineering is a good and efficient way to study dynamic processes in pharmacokinetics, because such integration combines mathematical rigor with biological insight.

There is no conflict of interest.

The author gratefully acknowledges the financial support obtained from the Slovak Academy of Sciences in Bratislava, Slovak Republic.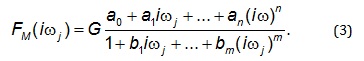

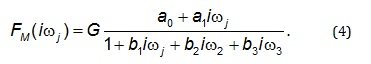
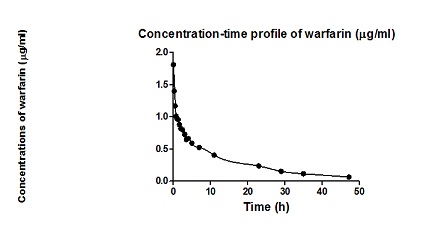
Figure 1: Observed plasma concentration time profile of warfarin and the description of the observed profile with the developed model of the dynamic system, mathematically describing the static and dynamic properties of the pharmacokinetic behavior of warfarin the subject investigated [1].

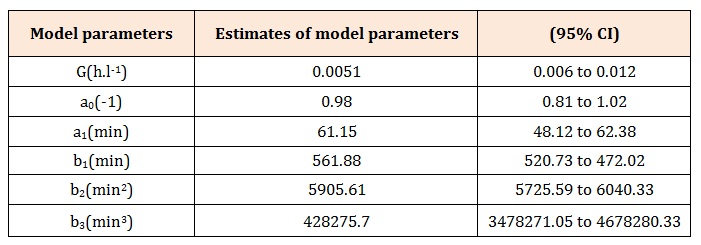
Table 1: Parameters of the third-order model of the dynamic system describing the pharmacokinetic behavior of intravenously administered warfarin in the subject investigated [1].

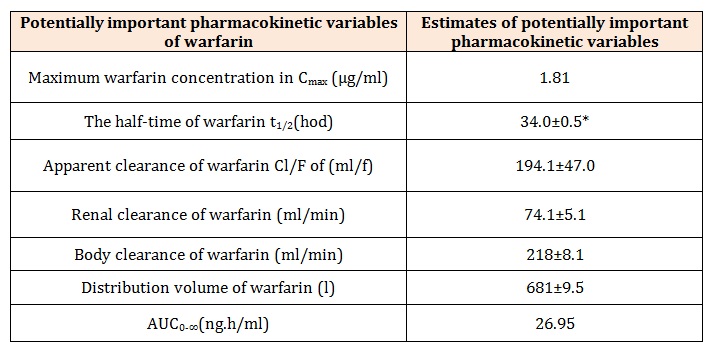
Table 2: Model-based estimates of potentially important pharmacokinetic variables of intravenously administered warfarin of the subject investiged [1].

*standard deviation